1 - Enlaces de Interés
1.1 - Enlace al profe del profe
2 - Grandes Matemáticos
2.1 - Georg Cantor. Teoría de conjuntos
3 - Videos Matemáticos
4 - Matemáticas: Juegos, Diversiones y Curiosidades
5 - Libros de Matemáticas
5.1 El hombre que calculaba
6 - Geometría
6.1 - Poliedros. Sólidos Platónicos
6.2 - Fractales
7 - Hojas de Problemas
7.1 - Hoja de Problemas 1.2
7.2 - Hoja de Problemas 1.3
7.3 - Hoja de Problemas 2.1
8 - Matemáticas y Arte
8.1 - Maurits Cornelis Escher
8.2 - Aleksandr Ródchenko
8.3 - Mosaicos y Teselaciones. Hueso Nazarí
8.4 - Fotografía Matemática
9 - Matemáticas y Tecnología
9.1 - Telecomunicaciones
TCP/IP, , HTTP, HTML
Vinton Cerf, Tim Berners-Lee
10 - Números Exstraordinarios
10.1 - El Número de Oro φ (fi)
Relación con la serie de Fibonacci
El número áureo en la Naturaleza
El número áureo en el ser humano
El número áureo en el Arte
El número áureo en la Música
10.2 - El Número π (pi)
10.3 - El Número e
jueves, 4 de junio de 2009
jueves, 21 de mayo de 2009
5 - Libros de Matemáticas
Libros de Matemáticas
El hombre que calculabaHank Tade-Mai es un viajero que retorna en su camello a Bagdad, luego de una excursión a la ciudad de Samarra. En su camino, encuentra a un hombre modestamente vestido, sentado en una piedra y exclamando en voz alta números gigantescos. El hombre que calculaba dice llamarse Beremiz Samir y cuenta que nació en Persia, donde trabajando como pastor comenzó a contar ovejas para no extraviar ninguna, siendo que a partir de entonces tomó el gusto por contar y calcular acerca de todo lo que encuentra a su paso. El viajero está maravillado con el don de este hombre y termina convenciéndolo, no sin antes sorprenderlo por su gran modestia, de ir a Bagdad para mostrar sus habilidades matemáticas y encontrar un trabajo bien pago en el gobierno del califa. Juntos, el viajero y Beremiz emprenden un largo viaje en el cual el hombre que calculaba resuelve diversos problemas, como disputas entre personas, y demuestra ser no sólo un prodigio matemático, sino también un hombre de una gran entereza moral y un excelente narrador de historias.
viernes, 24 de abril de 2009
9 - Matemáticas y Tecnología
Vinton Cerf y Berners-Lee son los creadores de Internet.
Vinton Cerf:
Vinton Cerf se licenció en Matemáticas y Ciencias de la Computación en la universidad de Stanford en 1965. Durante su estancia posterior en la Universidad de California (UCLA) se sacó el Máster en Ciencia y el Doctorado. En este periodo coincidió con un grupo de gente que estaba estudiando el desarrollo de la conmutación de paquetes, gracias al soporte económico de DARPA.
¿Qué es TCP/IP?
El TCP/IP es la base de Internet, y sirve para enlazar computadoras que utilizan diferentes sistemas operativos, incluyendo PC, minicomputadoras y computadoras centrales sobre redes de área local (LAN) y área extensa (WAN). TCP/IP fue desarrollado y demostrado por primera vez en 1972 por el Departamento de Defensa de los Estados Unidos, ejecutándolo en ARPANET, una red de área extensa de dicho departamento.
La familia de protocolos de Internet es un conjunto de protocolos de red en la que se basa Internet y que permiten la transmisión de datos entre redes de computadoras. En ocasiones se le denomina conjunto de protocolos TCP/IP, en referencia a los dos protocolos más importantes que la componen: Protocolo de Control de Transmisión (TCP) y Protocolo de Internet (IP), que fueron los dos primeros en definirse, y que son los más utilizados de la familia. Existen tantos protocolos en este conjunto que llegan a ser más de 100 diferentes, entre ellos se encuentra el popular HTTP (HyperText Transfer Protocol), que es el que se utiliza para acceder a las páginas web, además de otros como el ARP (Address Resolution Protocol) para la resolución de direcciones, el FTP (File Transfer Protocol) para transferencia de archivos, y el SMTP (Simple Mail Transfer Protocol) y el POP (Post Office Protocol) para correo electrónico, TELNET para acceder a equipos remotos, entre otros.
¿Qué es el http?
HTML, siglas de HyperText Markup Language (Lenguaje de Marcas de Hipertexto), es el lenguaje de marcado predominante para la construcción de páginas web. Es usado para describir la estructura y el contenido en forma de texto, así como para complementar el texto con objetos tales como imágenes. HTML se escribe en forma de "etiquetas", rodeadas por corchetes angulares
Vinton Cerf:
Vinton Cerf se licenció en Matemáticas y Ciencias de la Computación en la universidad de Stanford en 1965. Durante su estancia posterior en la Universidad de California (UCLA) se sacó el Máster en Ciencia y el Doctorado. En este periodo coincidió con un grupo de gente que estaba estudiando el desarrollo de la conmutación de paquetes, gracias al soporte económico de DARPA.
A principios de los 70, otro problema para el sistema de defensa norteamericano era que las diferentes redes de sus secciones eran de diferente tipo y sistemas operativos y eran necesario que se interconectasen y se entendiesen, creando así una "red de redes" . Las investigaciones, lideradas por Vinton Cerf primero desde la Universidad de California (1967-1972) y posteriormente desde la Universidad de Stanford (1972-1976), llevaron al diseño del conjunto de protocolos que hoy son conocidos como TCP/IP, que fue presentado por Vinton Cerf y Robert Kahn en 1972.
En DARPA promovió el desarrolo, basandose en la conmutación de paquetes y en los protocolos TCP/IP, de un conjunto de pequeños ordenadores que se denominaron ARPANET y que formarían el "embrión" de la red de redes.
Entre 1976 y 1982, trabajando en DARPA, fue pionero en el desarrollo de la transmisión por radio de paquetes, transmisión por satélite de paquetes, responsable del proyecto Internet y del programa de investigación de seguridad en la red. Siempre preocupado por los problemas de conexión de redes, Cerf estableció en 1979 la Internet Configurarion Control Board (que posteriormente se denominó Internet Activities Board) y fue su primer presidente.
También fue uno de los fundadores de la Internet Society y su primer presidente, en 1992.
Vinton Cerf es considerado como el "padre" de Internet.
BERNERS-LEE:
El padre de las 3 W.- Para presentar a Tim Berners-Lee sólo hacen falta decir tres palabras: World Wide Web. Y es que él no es ni más ni menos que el creador de WWW, el sistema que hace posible que conozcamos a Internet tal cual es hoy en día; además de seguir siendo director del Consorcio World Wide Web (W3C), luego de haber impulsado su creación hacia 1994.
Este británico que habita en los Estados Unidos, fue quien escribió el primer servidor World Wide Web, el Protocolo de transferencia de hipertexto (HTTP), concepto fundamental para la difusión masiva de Internet, en 1990.
Hijo de padres matemáticos, Berners-Lee nació el 8 de junio de 1955 en Londres y se graduó con la licenciatura en Física en el Queen’s College de la Universidad de Oxford, en Inglaterra, allá por 1976. Ya a principios de los 80 desarrolló un programa, el “Enquire”, la base de lo que sería su futura y máxima creación.
Pero fue en 1989 cuando le propuso al CERN (Laboratorio Europeo de Física de las Partículas) en Ginebra, su idea de un hipertexto global que se transformaría en la World Wide Web. Inicialmente, surgió como una forma de establecer una comunicación más fluida a través de Internet entre los mismos científicos.
Basándose en la idea de la universalidad del lenguaje, así fue como redactó el HTLM (HyperText Markup Language), el lenguaje que permite establecer enlaces con otros documentos en una máquina, y el esquema de direcciones que genera una localización única para cada página, URL (Uniform Resourse Locutor). Asimismo, redactó el HTTP (HyperText Transfer Protocol), que permite la trasferencia de la información en la red.
En 1991 publicó su proyecto para que comenzara a ser probado por otros y en sólo tres años, para 1994, ya se había difundido a pasos agigantados, pasando de 26 servidores web en 1992 a 200 en 1995.
Sin embargo, la falta de cooperación en Europa hizo que se trasladara a Estados Unidos, puntualmente al Computer Science (LCS) de Massachusetts Institute of Technology (MIT), en donde incluso conformó el Consorcio que actualmente coordina el desarrollo del World Wide Web, W3C, en donde estuvo al frente desde sus orígenes en 1994.
Este consorcio, que ya cuenta con más de 400 miembros a nivel mundial, elabora normas técnicas y establece estándares para la Red y sus aplicaciones.
En los últimos tiempos, Berners-Lee estaba trabajando en una Red semántica, una red que permitirá buscar la información en diversas bases de datos, todas compatibles, por lo que podrá ser manejada directamente por las computadoras. Además de hacer posible que los programas de búsqueda den los resultados justos y no como pasa actualmente, que frente a una búsqueda surgen cientos de resultados.
Pero mientras sigue investigando, su gran creación sigue siendo el puntal de la web universal y aquello que comenzó como una simple idea de conectar a algunos científicos a través de Internet actualmente ya cuenta con más de 100 millones de páginas. Para sacarse el sombrero delante de sir Tim Berners-Lee.¿Qué es TCP/IP?
El TCP/IP es la base de Internet, y sirve para enlazar computadoras que utilizan diferentes sistemas operativos, incluyendo PC, minicomputadoras y computadoras centrales sobre redes de área local (LAN) y área extensa (WAN). TCP/IP fue desarrollado y demostrado por primera vez en 1972 por el Departamento de Defensa de los Estados Unidos, ejecutándolo en ARPANET, una red de área extensa de dicho departamento.
La familia de protocolos de Internet es un conjunto de protocolos de red en la que se basa Internet y que permiten la transmisión de datos entre redes de computadoras. En ocasiones se le denomina conjunto de protocolos TCP/IP, en referencia a los dos protocolos más importantes que la componen: Protocolo de Control de Transmisión (TCP) y Protocolo de Internet (IP), que fueron los dos primeros en definirse, y que son los más utilizados de la familia. Existen tantos protocolos en este conjunto que llegan a ser más de 100 diferentes, entre ellos se encuentra el popular HTTP (HyperText Transfer Protocol), que es el que se utiliza para acceder a las páginas web, además de otros como el ARP (Address Resolution Protocol) para la resolución de direcciones, el FTP (File Transfer Protocol) para transferencia de archivos, y el SMTP (Simple Mail Transfer Protocol) y el POP (Post Office Protocol) para correo electrónico, TELNET para acceder a equipos remotos, entre otros.
¿Qué es el http?
El protocolo de transferencia de hipertexto (HTTP, HyperText Transfer Protocol) es el protocolo usado en cada transacción de la Web (WWW). HTTP fue desarrollado por el consorcio W3C y la IETF, colaboración que culminó en 1999 con la publicación de una serie de RFC, siendo el más importante de ellos el RFC 2616, que especifica la versión 1.1.
HTTP define la sintaxis y la semántica que utilizan los elementos software de la arquitectura web (clientes, servidores, proxies) para comunicarse. Es un protocolo orientado a transacciones y sigue el esquema petición-respuesta entre un cliente y un servidor. Al cliente que efectúa la petición (un navegador o un spider) se lo conoce como "user agent" (agente del usuario). A la información transmitida se la llama recurso y se la identifica mediante un URL. Los recursos pueden ser archivos, el resultado de la ejecución de un programa, una consulta a una base de datos, la traducción automática de un documento, etc.
HTML, siglas de HyperText Markup Language (Lenguaje de Marcas de Hipertexto), es el lenguaje de marcado predominante para la construcción de páginas web. Es usado para describir la estructura y el contenido en forma de texto, así como para complementar el texto con objetos tales como imágenes. HTML se escribe en forma de "etiquetas", rodeadas por corchetes angulares
HTML también puede describir, hasta un cierto punto, la apariencia de un documento, y puede incluir un script (por ejemplo Javascript), el cual puede afectar el comportamiento de navegadores web y otros procesadores de HTML.
HTML también es usado para referirse al contenido del tipo de MIME text/html o todavía más ampliamente como un término genérico para el HTML, ya sea en forma descendida del XML (como XHTML 1.0 y posteriores) o en forma descendida directamente de SGML (como HTML 4.01 y anteriores).
La telecomunicación (del prefijo griego tele, "distancia" o "lejos", "comunicación a distancia") es una técnica consistente en transmitir un mensaje desde un punto a otro, normalmente con el atributo típico adicional de ser bidireccional. El término telecomunicación cubre todas las formas de comunicación a distancia, incluyendo radio, telegrafía, televisión, telefonía, transmisión de datos e interconexión de ordenadores a nivel de enlace. El Día Mundial de la Telecomunicación se celebra el 17 de mayo.
La base matemática sobre la que se desarrollan las telecomunicaciones fue desarrollada por el físico inglés James Clerk Maxwell. Maxwell, en el prefacio de su obra Treatise on Electricity and Magnetism (1873), declaró que su principal tarea consistía en justificar matemáticamente conceptos físicos descritos hasta ese momento de forma únicamente cualitativa, como las leyes de la inducción electromagnética y de los campos de fuerza, enunciadas por Michael Faraday. Con este objeto, introdujo el concepto de onda electromagnética, que permite una descripción matemática adecuada de la interacción entre electricidad y magnetismo mediante sus célebres ecuaciones que describen y cuantifican los campos de fuerzas. Maxwell predijo que era posible propagar ondas por el espacio libre utilizando descargas eléctricas, hecho que corroboró Heinrich Hertz en 1887, ocho años después de la muerte de Maxwell, y que, posteriormente, supuso el inicio de la era de la comunicación rápida a distancia. Hertz desarrolló el primer transmisor de radio generando radiofrecuencias entre 31 MHz y 1.25 GHz.
viernes, 27 de marzo de 2009
10 - Números Exstraordinarios
NUMERO DE ORO
NUMERO E
El número áureo en el Ser Humano.
La Anatomía de los humanos se basa en una relación Φ estadística y aproximada, así vemos que:
El número áureo en el Arte.
Relaciones en la forma de la Gran Pirámide de Gizeh. La afirmación de Heródoto de que el cuadrado de la altura es igual a la superficie de una cara es posible únicamente si la semi-sección meridiana de la pirámide es proporcional al triángulo rectángulo
, donde 1 representa proporcionalmente a la mitad de la base, la raíz cuadrada del número áureo a la altura hasta el vértice inexistente y el número áureo o hipotenusa del triángulo a la apotema de la Gran Pirámide. Esta tesis ha sido defendida por los matemáticos Jarolimek, K. Kleppisch y W. A. Price (ver referencias), cuenta con el testimonio histórico de Heródoto y resulta teóricamente con sentido, aunque una construcción de semejante tamaño deba contener errores inevitables a toda obra arquitectónica y a la misma naturaleza de la tecnología humana, que en la práctica puede manejar únicamente números racionales. Los demás investigadores famosos se inclinan por la hipótesis de que los constructores intentaron una cuadratura del círculo, pues la raíz cuadrada del número áureo se aproxima mucho al cociente de 4 sobre π.
El número áureo en la Musica.
Es necesario aclarar que cuando se menciona al número áureo en una realización artística de cualquier naturaleza no se está haciendo mención al número áureo de los matemáticos, un irracional con infinitos decimales, sino a una aproximación racional adecuada a las circunstancias o a un dibujo hecho con regla no graduada de un solo borde y longitud indefinida y un compás de abertura fija o variable. Generalmente se utilizan cocientes de números pertenecientes a la sucesión de Fibonacci que dan valores aproximados, alternativamente por defecto o por exceso, según la necesidad o la sensibilidad humana y hasta la capacidad de separación tonal de cada instrumento. Un violín, por ejemplo, puede separar hasta un tercio de tono. El oído humano sano y entrenado distingue hasta trescientos sonidos por octava. Como un ejemplo conocido y no discutido tenemos a la escala atemperada o templada. Esta es una escala logarítmica. Se creó muy poco tiempo después de que los logaritmos pasaran al patrimonio de la matemática. La octava atemperada está basada en![\sqrt[12]{2}](http://upload.wikimedia.org/math/7/0/b/70b8b8fc763c20423a65bd934e378085.png)
. Este número irracional tiene infinitos decimales, pero la afinación se hace redondeando las cifras de las frecuencias a uno o dos decimales. De cualquier manera, el error tonal total cometido no es superior al doceavo de tono y el oído humano no lo nota.
El número áureo o de oro (también llamado número dorado, razón áurea, razón dorada, media áurea, proporción áurea y divina proporción) representado por la letra griega φ (fi) (en honor a Leonardo de Pisa Fibonacci), es el número irracional:
Se trata de un número algebraico que posee muchas propiedades interesantes y que fue descubierto en la antigüedad, no como “unidad” sino como relación o proporción. Esta proporción se encuentra tanto en algunas figuras geométricas como en la naturaleza en elementos tales como caracolas, nervaduras de las hojas de algunos árboles, el grosor de las ramas, etc.
Hagamos un experimento: con un papel y un lápiz dibuja una recta de la dimensión que quieras. Fíjate bien en ella y después divídela en dos partes desiguales mediante un pequeño trazo, de tal forma que los dos segmentos sean equilibrados y proporcionalmente agradables. Mídelos. Podrás verificar, entonces, que la menor es aproximadamente un 62 % de la mayor y que ésta es un 62% de la recta completa.
Fray Paciolo di Borgo, monje italiano, enuncia en el 1509 una fórmula matemática cuya aplicación da una constante a la que denominónúmero de oro, sección áurea, o divina proporción. Ya utilizada de forma empírica en la antigüedad, ésta Divina Relación se encuentra cuando, realizando el ejercicio anterior, el segmento menor está en la misma proporción con respecto al mayor que éste con respecto a la suma de ambos, es decir, con respecto al total. Este número equivale al 62% y es exactamente 0.618.
Curiosamente, esta proporción, considerada como la más armoniosa para la sensibilidad humana, se corresponde con las proporciones que nos presenta la naturaleza. La misma relación la encontramos entre las diferentes medidas de la cara, en las ramas de los árboles, en los cristales minerales, en las conchas marinas, en la relación entre los ejes mayor y menor de un huevo de gallina, etc.
Es sencillo comprobarlo, entre la anchura de la nariz y de la boca, o entre las distancias comprendidas desde el pelo de la frente hasta la base de la nariz y entre ésta y la barbilla, etc.
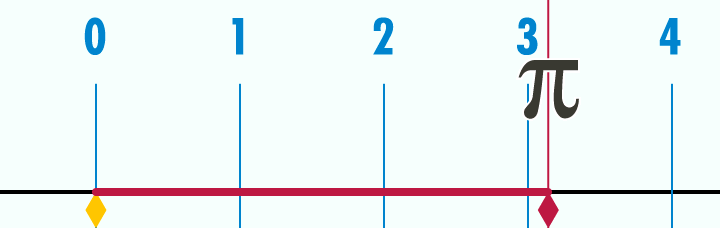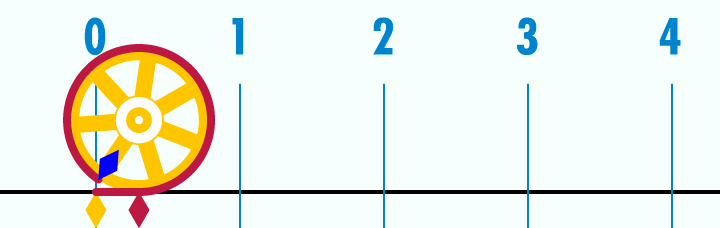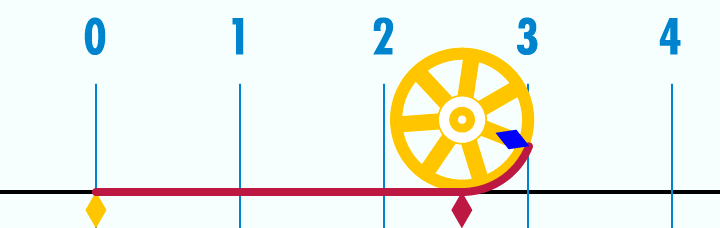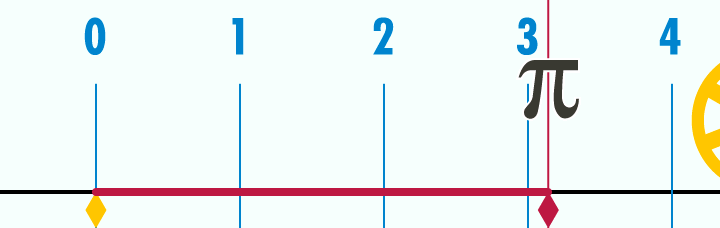
Deducimos de estas sorprendentes "coincidencias" que nuestra sensibilidad está condicionada ancestralmente por unas proporciones presentes en la naturaleza. Fruto de la observación humana a través de los tiempos, estas relaciones se han transformado en arquetipos, se han estereotipado. Por lo tanto, dada esta proporción, podemos entender que nuestra percepción de lo bello está supeditada a la armonía de las medidas, y explica que, a pesar de lo relativo del concepto de belleza, podamos considerar la existencia de algo próximo a la belleza absoluta.π (pi) es la relación entre la longitud de una circunferencia y su diámetro, en Geometría euclidiana. Es un número irracional y una de las constantes matemáticas más importantes. Se emplea frecuentemente en matemáticas, física e ingeniería. El valor numérico de π, truncado a sus primeras cifras, es el siguiente:
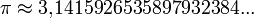
El valor de π se ha obtenido con diversas aproximaciones a lo largo de la historia, siendo una de las constantes matemáticas que más aparece en las ecuaciones de la física, junto con el número e. Por ello, tal vez sea la constante que más pasiones desata entre los matemáticos profesionales y aficionados. La relación entre la circunferencia y su diámetro no es constante en geometrías no euclídeas.
NUMERO E
La constante matemática e es el único número real que siendo usado como base de una función exponencial hace que la derivada de ésta en cualquier punto coincida con el valor de dicha función en ese punto. Así, la derivada de la función f(x) = ex es esa misma función. La función ex es también llamada función exponencial, y su función inversa es el logaritmo natural, también llamado logaritmo en base e o logaritmo neperiano.
El número e es uno de los números más importantes en la matemática,[1] junto con el número π, la unidad imaginaria i y el 0 y el 1, por ser los elementos neutros de la adición y la multiplicación, respectivamente. Curiosamente, la identidad de Euler los relaciona (eiπ+1=0) de manera asombrosa. Además, en virtud de la fórmula de Euler, es posible expresar cualquier número complejo en notación exponencial.
A diferencia de lo que se cree, el número e no se llama número de Euler. Su nombre correcto es la constante de Neper, en honor al matemático escocés John Napier, quien introdujo el concepto de logaritmo al cálculo matemático. La constante e no debe ser confundida con γ, la constante de Euler-Mascheroni, a la que a veces se hace referencia como constante de Euler.
El número áureo en la Naturaleza.
- La relación entre la cantidad de abejas macho y abejas hembra en un panal.
- La disposición de los pétalos de las flores (el papel del número áureo en la botánica recibe el nombre de Ley de Ludwig).
- La distribución de las hojas en un tallo. Ver: Sucesión de Fibonacci.
- La relación entre las nervaduras de las hojas de los árboles
- La relación entre el grosor de las ramas principales y el tronco, o entre las ramas principales y las secundarias (el grosor de una equivale a Φ tomando como unidad la rama superior).
- La distancia entre las espirales de una Piña.
El número áureo en el Ser Humano.
La Anatomía de los humanos se basa en una relación Φ estadística y aproximada, así vemos que:
- La relación entre la altura de un ser humano y la altura de su ombligo.
- La relación entre la distancia del hombro a los dedos y la distancia del codo a los dedos.
- La relación entre la altura de la cadera y la altura de la rodilla.
- La relación entre el primer hueso de los dedos (metacarpiano) y la primera falange, o entre la primera y la segunda, o entre la segunda y la tercera, si dividimos todo es Φ.
- La relación entre el diámetro de la boca y el de la nariz
- Es Φ la relación entre el diámetro externo de los ojos y la línea inter-pupilar
- Cuando la tráquea se divide en sus bronquios, si se mide el diámetro de los bronquios por el de la tráquea se obtiene Φ, o el de la aorta con sus dos ramas terminales.
El número áureo en el Arte.
Relaciones en la forma de la Gran Pirámide de Gizeh. La afirmación de Heródoto de que el cuadrado de la altura es igual a la superficie de una cara es posible únicamente si la semi-sección meridiana de la pirámide es proporcional al triángulo rectángulo
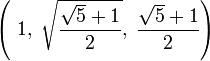, donde 1 representa proporcionalmente a la mitad de la base, la raíz cuadrada del número áureo a la altura hasta el vértice inexistente y el número áureo o hipotenusa del triángulo a la apotema de la Gran Pirámide. Esta tesis ha sido defendida por los matemáticos Jarolimek, K. Kleppisch y W. A. Price (ver referencias), cuenta con el testimonio histórico de Heródoto y resulta teóricamente con sentido, aunque una construcción de semejante tamaño deba contener errores inevitables a toda obra arquitectónica y a la misma naturaleza de la tecnología humana, que en la práctica puede manejar únicamente números racionales. Los demás investigadores famosos se inclinan por la hipótesis de que los constructores intentaron una cuadratura del círculo, pues la raíz cuadrada del número áureo se aproxima mucho al cociente de 4 sobre π.El número áureo en la Musica.
Es necesario aclarar que cuando se menciona al número áureo en una realización artística de cualquier naturaleza no se está haciendo mención al número áureo de los matemáticos, un irracional con infinitos decimales, sino a una aproximación racional adecuada a las circunstancias o a un dibujo hecho con regla no graduada de un solo borde y longitud indefinida y un compás de abertura fija o variable. Generalmente se utilizan cocientes de números pertenecientes a la sucesión de Fibonacci que dan valores aproximados, alternativamente por defecto o por exceso, según la necesidad o la sensibilidad humana y hasta la capacidad de separación tonal de cada instrumento. Un violín, por ejemplo, puede separar hasta un tercio de tono. El oído humano sano y entrenado distingue hasta trescientos sonidos por octava. Como un ejemplo conocido y no discutido tenemos a la escala atemperada o templada. Esta es una escala logarítmica. Se creó muy poco tiempo después de que los logaritmos pasaran al patrimonio de la matemática. La octava atemperada está basada en
. Este número irracional tiene infinitos decimales, pero la afinación se hace redondeando las cifras de las frecuencias a uno o dos decimales. De cualquier manera, el error tonal total cometido no es superior al doceavo de tono y el oído humano no lo nota.
jueves, 15 de enero de 2009
HOJA DE MATEMATICAS 2.1
Hoja de matemáticas 1.3
wladimir Alejandro Muñoz Castro
1) ¿De cuántas formas diferentes se pueden juntar 8€ utilizando solo monedas de 2€, 1€ y 0.50 €?.
2) Un motorista sale de su casa para acudir a una cita. Se da cuenta de que si viaja a 60 km/h llegará un cuarto de hora tarde, pero si lo hace a 100 km/h llegará un cuarto de hora antes. ¿A qué distancia está su destino?.
1/4 100 = 25 Km 100-25 = 75 Km/h1/4 60 = 15 Km 60 + 15 = 75 Km/hS = V x T 75 x 1100 x 3/460 x 5/4
4) Utilizando solamente la cifra 5 y las operaciones oportunas se puede obtener cualquier número.
Por ejemplo, para obtener 6 podemos hacer:55: 5 – 5 = 6
Busca la manera de obtener con la mínima cantidad de cincos:
a) Los veinte primeros números naturales.
b)Los números 111 y 125.c) Los números 500, 1000 y 3000.
5) Un nenúfar, en un lago, dobla su tamaño todos los días. En un mes cubre todo el lago. ¿Cuánto tiempo tardarán dos nenúfares en cubrir todo el lago?.
6) ¿Son ciertas las siguientes afirmaciones? Razona tus respuestas.
a) La suma de dos números consecutivos no es múltiplo de dos.
b) La suma de dos impares consecutivos no es múltiplo de cuatro.
c) La suma de tres números naturales consecutivos es múltiplo de tres.
7) ¿Cuántos capicúas existen de cuatro cifras en los que las dos cifras extremas suman lo mismo que las dos centrales?.
8) ¿Cuántos tramos de carretera son necesarios para comunicar cuatro ciudades de forma que desde cada una se pueda llegar a cualquier otra sin pasar por una tercera? ¿Y para comunicar cinco ciudades?¿Y para comunicar n ciudades?.
9) Un grupo de amigos va a comer a un restaurante chino. Cada dos comparten un plato de arroz, cada 3 uno de salsa y cada cuatro uno de carne. En total se sirvieron 65 platos. ¿Cuántos amigos fueron a comer?.
10) ¿En cuantos ceros acaba el número 125!?.
1!= 1
2!= 2x1
3!= 3x2x1
4!= 4x3x2x1
5!= 5x4x3x2x1
10!= 10x9x8...3x2x1
125!= 125x124x123...3x2x1
11) ¿Cuál es el último dígito de la expresión 2 (elevado a la 103) + 3?.
2 (elevado a la 103) + 3
2 (elevado a la 0) = 1
2 (elevado a la 1) = 2
2 (elevado a la 2) = 4
2 (elevado a la 3) = 8
2 (elevado a la 4) = 16
2 (elevado a la 5) = 32
2 (elevado a la 6) = 64
2 (elevado a la 7) = 128
2 (elevado a la 8) = 256
2 (elevado a la 9) = 512
2 (elevado a la 10)= 1024
2 (elevado a la 11)= 2048
Terminaciones en: 2486
12) De los 30 alumnos y alumnas de una clase, 15 declaran ser aficionados al rock, y 13, al bacalao. Hay 6 de ellos que son aficionados a ambos ritmos musicales. ¿Cuántos no son aficionados ni a lo uno ni a lo otro?.
Un calendario con dos cubos
¿Es posible construir un calendario con dos cubos?
wladimir Alejandro Muñoz Castro
1) ¿De cuántas formas diferentes se pueden juntar 8€ utilizando solo monedas de 2€, 1€ y 0.50 €?.
2) Un motorista sale de su casa para acudir a una cita. Se da cuenta de que si viaja a 60 km/h llegará un cuarto de hora tarde, pero si lo hace a 100 km/h llegará un cuarto de hora antes. ¿A qué distancia está su destino?.
1/4 100 = 25 Km 100-25 = 75 Km/h1/4 60 = 15 Km 60 + 15 = 75 Km/hS = V x T 75 x 1100 x 3/460 x 5/4
4) Utilizando solamente la cifra 5 y las operaciones oportunas se puede obtener cualquier número.
Por ejemplo, para obtener 6 podemos hacer:55: 5 – 5 = 6
Busca la manera de obtener con la mínima cantidad de cincos:
a) Los veinte primeros números naturales.
b)Los números 111 y 125.c) Los números 500, 1000 y 3000.
5) Un nenúfar, en un lago, dobla su tamaño todos los días. En un mes cubre todo el lago. ¿Cuánto tiempo tardarán dos nenúfares en cubrir todo el lago?.
6) ¿Son ciertas las siguientes afirmaciones? Razona tus respuestas.
a) La suma de dos números consecutivos no es múltiplo de dos.
b) La suma de dos impares consecutivos no es múltiplo de cuatro.
c) La suma de tres números naturales consecutivos es múltiplo de tres.
7) ¿Cuántos capicúas existen de cuatro cifras en los que las dos cifras extremas suman lo mismo que las dos centrales?.
8) ¿Cuántos tramos de carretera son necesarios para comunicar cuatro ciudades de forma que desde cada una se pueda llegar a cualquier otra sin pasar por una tercera? ¿Y para comunicar cinco ciudades?¿Y para comunicar n ciudades?.
9) Un grupo de amigos va a comer a un restaurante chino. Cada dos comparten un plato de arroz, cada 3 uno de salsa y cada cuatro uno de carne. En total se sirvieron 65 platos. ¿Cuántos amigos fueron a comer?.
10) ¿En cuantos ceros acaba el número 125!?.
1!= 1
2!= 2x1
3!= 3x2x1
4!= 4x3x2x1
5!= 5x4x3x2x1
10!= 10x9x8...3x2x1
125!= 125x124x123...3x2x1
11) ¿Cuál es el último dígito de la expresión 2 (elevado a la 103) + 3?.
2 (elevado a la 103) + 3
2 (elevado a la 0) = 1
2 (elevado a la 1) = 2
2 (elevado a la 2) = 4
2 (elevado a la 3) = 8
2 (elevado a la 4) = 16
2 (elevado a la 5) = 32
2 (elevado a la 6) = 64
2 (elevado a la 7) = 128
2 (elevado a la 8) = 256
2 (elevado a la 9) = 512
2 (elevado a la 10)= 1024
2 (elevado a la 11)= 2048
Terminaciones en: 2486
12) De los 30 alumnos y alumnas de una clase, 15 declaran ser aficionados al rock, y 13, al bacalao. Hay 6 de ellos que son aficionados a ambos ritmos musicales. ¿Cuántos no son aficionados ni a lo uno ni a lo otro?.
Un calendario con dos cubos
¿Es posible construir un calendario con dos cubos?
viernes, 12 de diciembre de 2008
6 - GEOMETRÌA
SOLIDOS PLATONICOS: Aqui os dejo una pagina chula de sobre los solidos platonicos tambien llamados cuerpos platonicos; http://www.luventicus.org/articulos/03Tr001/index.html
Los sólidos platónicos, también conocidos como cuerpos platónicos, cuerpos cósmicos, sólidos pitagóricos, sólidos perfectos, poliedros de Platón o, con más precisión, poliedros regulares convexos; son cuerpos geométricos caracterizados por ser poliedros convexos cuyas caras son polígonos regulares iguales y en cuyos vértices se unen el mismo número de caras.
FRACTALES:Un fractal natural es un elemento de la naturaleza que puede ser descrito mediante la geometría fractal. Las nubes, las montañas, el sistema circulatorio, las líneas costeras o los copos de nieve son fractales naturales. Esta representación es aproximada, pues las propiedades atribuidas a los objetos fractales ideales, como el detalle infinito, tienen límites en el mundo natural.
Los sólidos platónicos, también conocidos como cuerpos platónicos, cuerpos cósmicos, sólidos pitagóricos, sólidos perfectos, poliedros de Platón o, con más precisión, poliedros regulares convexos; son cuerpos geométricos caracterizados por ser poliedros convexos cuyas caras son polígonos regulares iguales y en cuyos vértices se unen el mismo número de caras.
FRACTALES:Un fractal natural es un elemento de la naturaleza que puede ser descrito mediante la geometría fractal. Las nubes, las montañas, el sistema circulatorio, las líneas costeras o los copos de nieve son fractales naturales. Esta representación es aproximada, pues las propiedades atribuidas a los objetos fractales ideales, como el detalle infinito, tienen límites en el mundo natural.
jueves, 11 de diciembre de 2008
8 - MATEMATICAS Y ARTE
Alexander Rodchenko
href="https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjDXi5rnPOuMZ4Vc7DRvqEr6JifazKanvWQFvbSB6hcIBdKN2r-9lksP-lIfexNzx0zkU7X-QBOUrxyXfGNqL8A9C9GXGlf1rVmIHeRooT3WSuupV_F1o6MZ0vftahGTg-SbDmSVbnmkbw/s1600-h/rodchenko_productionist_uni.jpg">
El trabajo fotográfico de Alexander Rodchenko se desarrolla en la URSS en una época de gran actividad creadora en la Europa occidental.Y al igual que los creadores occidentales, Rodchenko indaga nuevas formas estilísticas.Sus imágenes presentan una parte de la historia de la URSS en la primera mitad del siglo XX.Sus imágenes poseen una fuerza extraordinaria, son contundentes.¿ A qué es debida esta fuerza ?Pienso que al riesgo con que realiza cada una de sus tomas. Al punto de vista que incluye en sus fotografías. A la forzada composición de cada una de sus imágenes. A sus picados y contra-picados.Es un admirador de la tecnología y en especial de todo lo que vuela: aviones, dirigibles, globos. De los puentes, torres metálicas y de la arquitectura.La tecnología representa el mundo contemporáneo.Para él, la ciudad moderna con los altos edificios con cristales en sus muros, la industria, los tranvías, los coches, los anuncios publicitarios, los barcos y aviones necesitan un cambio en la percepción visual.Los puntos de vista más interesantes para mostrar la realidad ya no es la vista horizontal de un hombre de pie, sino de abajo arriba y de arriba abajo, con el horizonte inclinado, lo que hace que la imágen adquiera mayor movimiento y dinamismo.Es un ejemplo nítido de lo que viene a denominarse estilo en un fotógrafo. Sus fotografías son fácilmente identificables.Estas composiciones las consigue cuando puede deshacerse de la servidumbre de las pesadas y rígidas cámaras de placas y al igual que otros fotógrafos consigue tener en sus manos las ligeras cámaras portátiles.En los retratos evita el manierismo propio de los estudios de fotografía. Sus retratos se convierten en símbolos, en iconos, al eliminar todo lo superfluo. En el retrato de la madre deja sólo la cabeza, el pañuelo y la mano sujetando las gafas.El poder expresivo de una fotografía depende tanto de los medios explicativos empleados como del sujeto descrito.BIOGRAFÍAAlexander Rodchenko nace en 1891 San Petersburgo.Estudia artes gráficas y pintura.En 1917 es coordinador del sindicato de artistas pintores.Trabaja en diferentes campos artísticos a lo largo de su vida: pintura, artes gráficas, escultura, arquitectura, diseño y fotografía. Es un artista completo.En 1920 es miembro de Inkhouk (Instituto de Cultura Artística).Pertenece a la vanguardia rusa, resultante de la revolución rusa de 1917.En 1923 trabaja para el cine. Concibe las películas de actualidad para la revista Kinopravda.Según sus palabras el fotomontaje le acerca a la fotografía.Se inicia en la fotografía a una edad adulta, a los 33 años, a partir del 1924 y hasta 1954.Comienza a fotografiar con una cámara de placas, pero comienza su verdadera producción cuando consigue una cámara portátil.Forma parte activamente del círculo de artistas que se reunen alrededor de la revista LEF que recoge discusiones sobre cine, arquitectura, literatura, teatro y decoración.Entre 1935 y 1941 realiza reportajes sobre los desfiles deportivos en la Plaza Roja y las series de fotografía sobre Moscú y el Circo.En 1944 es director artístico de la Casa de la Técnica en Moscú.En 1956 muere en Moscú.
Maurits Cornelis Escher
Escher nació un 17 de Junio de 1898 en Leeuwarden (Holanda). Como la mayoría de los genios, no fue un estudiante destacado en el colegio, a pesar de lo cual su talento artístico ya se vislumbraba en este periodo. Su padre le introdujo al mundo de la carpintería y le enseño otras habilidades manuales. Comenzó los estudios de Arquitectura, pero una vez allí, Escher se dió cuenta de que su auténtica pasión eran las artes gráficas. Tras dos años en la escuela de arte, obtuvo una especialización en técnicas gráficas y trabajo sobre madera y se dedicó a viajar por el sur de Francia, España e Italia, lugares donde encontró numerosas fuentes de inspiración para su obra. A lo largo de su carrera como artista, Escher se centró en el arte de la estructura, rama hacía la que sentía una especial atracción. Sin embargo, sus primeras obras tendieron a retratar de forma realista los paisajes y la arquitectura con los que se encontró en sus viajes. En estos trabajos Escher reflejó su predilección por la estructura de las construcciones en detrimento del paisaje en sí. La Alhambra de Granada (España), visitada por Escher en incontables ocasiones, fue el edificio que impresionó de forma definitiva a nuestro personaje gracias a las recargadas ornamentaciones moriscas de sus muros, las cuales se repartían el espacio disponible de forma esquemática y perfecta. Esta cautivación le influyó en sus creaciones posteriores a 1937, en las que muestran una división regular del plano y sus famosos patrones de repetición. Su visión única del espacio y de las matemáticas le permitieron dibujar una numerosa colección de fantásticos dibujos hasta su muerte en 1972.
Hueso Nazarì
href="https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjDXi5rnPOuMZ4Vc7DRvqEr6JifazKanvWQFvbSB6hcIBdKN2r-9lksP-lIfexNzx0zkU7X-QBOUrxyXfGNqL8A9C9GXGlf1rVmIHeRooT3WSuupV_F1o6MZ0vftahGTg-SbDmSVbnmkbw/s1600-h/rodchenko_productionist_uni.jpg">
El trabajo fotográfico de Alexander Rodchenko se desarrolla en la URSS en una época de gran actividad creadora en la Europa occidental.Y al igual que los creadores occidentales, Rodchenko indaga nuevas formas estilísticas.Sus imágenes presentan una parte de la historia de la URSS en la primera mitad del siglo XX.Sus imágenes poseen una fuerza extraordinaria, son contundentes.¿ A qué es debida esta fuerza ?Pienso que al riesgo con que realiza cada una de sus tomas. Al punto de vista que incluye en sus fotografías. A la forzada composición de cada una de sus imágenes. A sus picados y contra-picados.Es un admirador de la tecnología y en especial de todo lo que vuela: aviones, dirigibles, globos. De los puentes, torres metálicas y de la arquitectura.La tecnología representa el mundo contemporáneo.Para él, la ciudad moderna con los altos edificios con cristales en sus muros, la industria, los tranvías, los coches, los anuncios publicitarios, los barcos y aviones necesitan un cambio en la percepción visual.Los puntos de vista más interesantes para mostrar la realidad ya no es la vista horizontal de un hombre de pie, sino de abajo arriba y de arriba abajo, con el horizonte inclinado, lo que hace que la imágen adquiera mayor movimiento y dinamismo.Es un ejemplo nítido de lo que viene a denominarse estilo en un fotógrafo. Sus fotografías son fácilmente identificables.Estas composiciones las consigue cuando puede deshacerse de la servidumbre de las pesadas y rígidas cámaras de placas y al igual que otros fotógrafos consigue tener en sus manos las ligeras cámaras portátiles.En los retratos evita el manierismo propio de los estudios de fotografía. Sus retratos se convierten en símbolos, en iconos, al eliminar todo lo superfluo. En el retrato de la madre deja sólo la cabeza, el pañuelo y la mano sujetando las gafas.El poder expresivo de una fotografía depende tanto de los medios explicativos empleados como del sujeto descrito.BIOGRAFÍAAlexander Rodchenko nace en 1891 San Petersburgo.Estudia artes gráficas y pintura.En 1917 es coordinador del sindicato de artistas pintores.Trabaja en diferentes campos artísticos a lo largo de su vida: pintura, artes gráficas, escultura, arquitectura, diseño y fotografía. Es un artista completo.En 1920 es miembro de Inkhouk (Instituto de Cultura Artística).Pertenece a la vanguardia rusa, resultante de la revolución rusa de 1917.En 1923 trabaja para el cine. Concibe las películas de actualidad para la revista Kinopravda.Según sus palabras el fotomontaje le acerca a la fotografía.Se inicia en la fotografía a una edad adulta, a los 33 años, a partir del 1924 y hasta 1954.Comienza a fotografiar con una cámara de placas, pero comienza su verdadera producción cuando consigue una cámara portátil.Forma parte activamente del círculo de artistas que se reunen alrededor de la revista LEF que recoge discusiones sobre cine, arquitectura, literatura, teatro y decoración.Entre 1935 y 1941 realiza reportajes sobre los desfiles deportivos en la Plaza Roja y las series de fotografía sobre Moscú y el Circo.En 1944 es director artístico de la Casa de la Técnica en Moscú.En 1956 muere en Moscú.
Maurits Cornelis Escher
Escher nació un 17 de Junio de 1898 en Leeuwarden (Holanda). Como la mayoría de los genios, no fue un estudiante destacado en el colegio, a pesar de lo cual su talento artístico ya se vislumbraba en este periodo. Su padre le introdujo al mundo de la carpintería y le enseño otras habilidades manuales. Comenzó los estudios de Arquitectura, pero una vez allí, Escher se dió cuenta de que su auténtica pasión eran las artes gráficas. Tras dos años en la escuela de arte, obtuvo una especialización en técnicas gráficas y trabajo sobre madera y se dedicó a viajar por el sur de Francia, España e Italia, lugares donde encontró numerosas fuentes de inspiración para su obra. A lo largo de su carrera como artista, Escher se centró en el arte de la estructura, rama hacía la que sentía una especial atracción. Sin embargo, sus primeras obras tendieron a retratar de forma realista los paisajes y la arquitectura con los que se encontró en sus viajes. En estos trabajos Escher reflejó su predilección por la estructura de las construcciones en detrimento del paisaje en sí. La Alhambra de Granada (España), visitada por Escher en incontables ocasiones, fue el edificio que impresionó de forma definitiva a nuestro personaje gracias a las recargadas ornamentaciones moriscas de sus muros, las cuales se repartían el espacio disponible de forma esquemática y perfecta. Esta cautivación le influyó en sus creaciones posteriores a 1937, en las que muestran una división regular del plano y sus famosos patrones de repetición. Su visión única del espacio y de las matemáticas le permitieron dibujar una numerosa colección de fantásticos dibujos hasta su muerte en 1972.
Hueso Nazarì
Suscribirse a:
Entradas (Atom)
