10 - Números Exstraordinarios

NUMERO DE ORO

El número áureo o de oro (también llamado número dorado, razón áurea, razón dorada, media áurea, proporción áurea y divina proporción) representado por la letra griega φ (fi) (en honor a Leonardo de Pisa Fibonacci), es el número irracional:

Se trata de un número algebraico que posee muchas propiedades interesantes y que fue descubierto en la antigüedad, no como “unidad” sino como relación o proporción. Esta proporción se encuentra tanto en algunas figuras geométricas como en la naturaleza en elementos tales como caracolas, nervaduras de las hojas de algunos árboles, el grosor de las ramas, etc.

Hagamos un experimento: con un papel y un lápiz dibuja una recta de la dimensión que quieras. Fíjate bien en ella y después divídela en dos partes desiguales mediante un pequeño trazo, de tal forma que los dos segmentos sean equilibrados y proporcionalmente agradables. Mídelos. Podrás verificar, entonces, que la menor es aproximadamente un 62 % de la mayor y que ésta es un 62% de la recta completa.

Fray Paciolo di Borgo, monje italiano, enuncia en el 1509 una fórmula matemática cuya aplicación da una constante a la que denominónúmero de oro, sección áurea, o divina proporción. Ya utilizada de forma empírica en la antigüedad, ésta Divina Relación se encuentra cuando, realizando el ejercicio anterior, el segmento menor está en la misma proporción con respecto al mayor que éste con respecto a la suma de ambos, es decir, con respecto al total. Este número equivale al 62% y es exactamente 0.618.

Curiosamente, esta proporción, considerada como la más armoniosa para la sensibilidad humana, se corresponde con las proporciones que nos presenta la naturaleza. La misma relación la encontramos entre las diferentes medidas de la cara, en las ramas de los árboles, en los cristales minerales, en las conchas marinas, en la relación entre los ejes mayor y menor de un huevo de gallina, etc.

Es sencillo comprobarlo, entre la anchura de la nariz y de la boca, o entre las distancias comprendidas desde el pelo de la frente hasta la base de la nariz y entre ésta y la barbilla, etc.

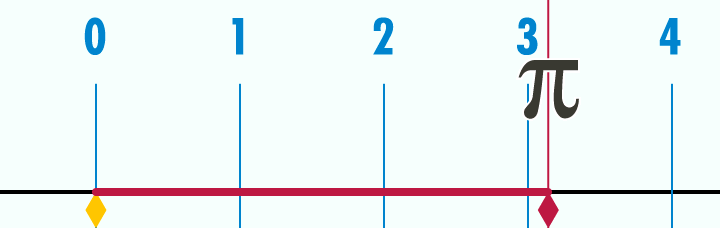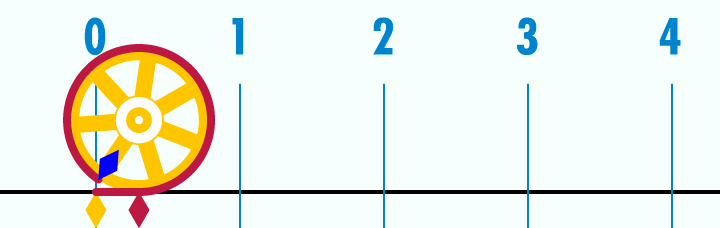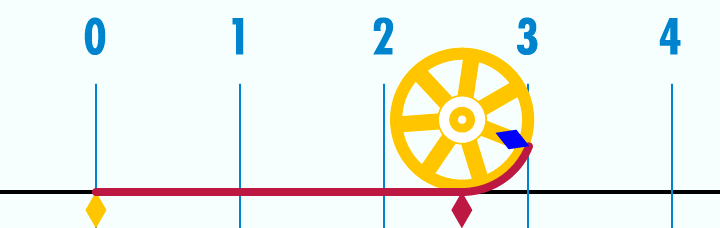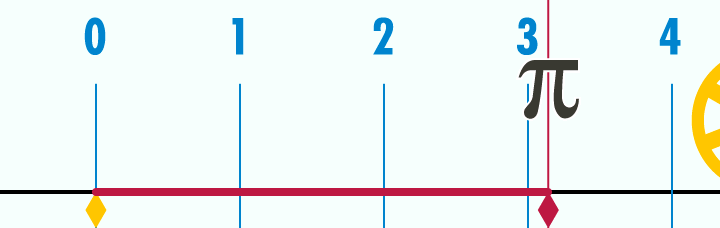
Deducimos de estas sorprendentes "coincidencias" que nuestra sensibilidad está condicionada ancestralmente por unas proporciones presentes en la naturaleza. Fruto de la observación humana a través de los tiempos, estas relaciones se han transformado en arquetipos, se han estereotipado. Por lo tanto, dada esta proporción, podemos entender que nuestra percepción de lo bello está supeditada a la armonía de las medidas, y explica que, a pesar de lo relativo del concepto de belleza, podamos considerar la existencia de algo próximo a la belleza absoluta.

El Número π

π (pi) es la relación entre la longitud de una circunferencia y su diámetro, en Geometría euclidiana. Es un número irracional y una de las constantes matemáticas más importantes. Se emplea frecuentemente en matemáticas, física e ingeniería. El valor numérico de π, truncado a sus primeras cifras, es el siguiente:

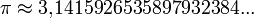
El valor de π se ha obtenido con diversas aproximaciones a lo largo de la historia, siendo una de las constantes matemáticas que más aparece en las ecuaciones de la física, junto con el número e. Por ello, tal vez sea la constante que más pasiones desata entre los matemáticos profesionales y aficionados. La relación entre la circunferencia y su diámetro no es constante en geometrías no euclídeas.

NUMERO E

La constante matemática e es el único número real que siendo usado como base de una función exponencial hace que la derivada de ésta en cualquier punto coincida con el valor de dicha función en ese punto. Así, la derivada de la función f(x) = e^x es esa misma función. La función e^x es también llamada función exponencial, y su función inversa es el logaritmo natural, también llamado logaritmo en base e o logaritmo neperiano.

El número e es uno de los números más importantes en la matemática,^[1] junto con el número π, la unidad imaginaria i y el 0 y el 1, por ser los elementos neutros de la adición y la multiplicación, respectivamente. Curiosamente, la identidad de Euler los relaciona (e^iπ+1=0) de manera asombrosa. Además, en virtud de la fórmula de Euler, es posible expresar cualquier número complejo en notación exponencial.

A diferencia de lo que se cree, el número e no se llama número de Euler. Su nombre correcto es la constante de Neper, en honor al matemático escocés John Napier, quien introdujo el concepto de logaritmo al cálculo matemático. La constante e no debe ser confundida con γ, la constante de Euler-Mascheroni, a la que a veces se hace referencia como constante de Euler.

El número áureo en la Naturaleza.

• La relación entre la cantidad de abejas macho y abejas hembra en un panal.
• La disposición de los pétalos de las flores (el papel del número áureo en la botánica recibe el nombre de Ley de Ludwig).
• La distribución de las hojas en un tallo. Ver: Sucesión de Fibonacci.
• La relación entre las nervaduras de las hojas de los árboles
• La relación entre el grosor de las ramas principales y el tronco, o entre las ramas principales y las secundarias (el grosor de una equivale a Φ tomando como unidad la rama superior).
• La distancia entre las espirales de una Piña.

La relación entre la distancia entre las espiras del interior espiralado de cualquier caracol o de cefalópodos como el nautilus hay por lo menos tres espirales logarítmicas más o menos asimilables a proporciones aúreas.



El número áureo en el Ser Humano.


La Anatomía de los humanos se basa en una relación Φ estadística y aproximada, así vemos que:

• La relación entre la altura de un ser humano y la altura de su ombligo.
• La relación entre la distancia del hombro a los dedos y la distancia del codo a los dedos.
• La relación entre la altura de la cadera y la altura de la rodilla.
• La relación entre el primer hueso de los dedos (metacarpiano) y la primera falange, o entre la primera y la segunda, o entre la segunda y la tercera, si dividimos todo es Φ.
• La relación entre el diámetro de la boca y el de la nariz
• Es Φ la relación entre el diámetro externo de los ojos y la línea inter-pupilar
• Cuando la tráquea se divide en sus bronquios, si se mide el diámetro de los bronquios por el de la tráquea se obtiene Φ, o el de la aorta con sus dos ramas terminales.

El número áureo en el Arte.



Relaciones en la forma de la Gran Pirámide de Gizeh. La afirmación de Heródoto de que el cuadrado de la altura es igual a la superficie de una cara es posible únicamente si la semi-sección meridiana de la pirámide es proporcional al triángulo rectángulo 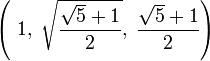, donde 1 representa proporcionalmente a la mitad de la base, la raíz cuadrada del número áureo a la altura hasta el vértice inexistente y el número áureo o hipotenusa del triángulo a la apotema de la Gran Pirámide. Esta tesis ha sido defendida por los matemáticos Jarolimek, K. Kleppisch y W. A. Price (ver referencias), cuenta con el testimonio histórico de Heródoto y resulta teóricamente con sentido, aunque una construcción de semejante tamaño deba contener errores inevitables a toda obra arquitectónica y a la misma naturaleza de la tecnología humana, que en la práctica puede manejar únicamente números racionales. Los demás investigadores famosos se inclinan por la hipótesis de que los constructores intentaron una cuadratura del círculo, pues la raíz cuadrada del número áureo se aproxima mucho al cociente de 4 sobre π.


El número áureo en la Musica.


Es necesario aclarar que cuando se menciona al número áureo en una realización artística de cualquier naturaleza no se está haciendo mención al número áureo de los matemáticos, un irracional con infinitos decimales, sino a una aproximación racional adecuada a las circunstancias o a un dibujo hecho con regla no graduada de un solo borde y longitud indefinida y un compás de abertura fija o variable. Generalmente se utilizan cocientes de números pertenecientes a la sucesión de Fibonacci que dan valores aproximados, alternativamente por defecto o por exceso, según la necesidad o la sensibilidad humana y hasta la capacidad de separación tonal de cada instrumento. Un violín, por ejemplo, puede separar hasta un tercio de tono. El oído humano sano y entrenado distingue hasta trescientos sonidos por octava. Como un ejemplo conocido y no discutido tenemos a la escala atemperada o templada. Esta es una escala logarítmica. Se creó muy poco tiempo después de que los logaritmos pasaran al patrimonio de la matemática. La octava atemperada está basada en . Este número irracional tiene infinitos decimales, pero la afinación se hace redondeando las cifras de las frecuencias a uno o dos decimales. De cualquier manera, el error tonal total cometido no es superior al doceavo de tono y el oído humano no lo nota.